Matrices and Vectors【矩阵和向量】
在$\begin{bmatrix}{1402}&{191}\\{1371}&{821}\\{949}&{1437}\\{147}&{1448}\end{bmatrix}$中,这是一个这个是4×2矩阵,即4行2列,如$m$为行,$n$为列,那么$m×n$即4×2,其中$A_{ij}$指第$i$行,第$j$列的元素。
向量是一种特殊的矩阵,向量一般都是列向量,如:$y=\left[ \begin{matrix} {460} \ {232} \ {315} \ {178} \\\end{matrix} \right]$为四维列向量(4×1)。
Addition and Scalar Multiplication【加法和标量乘法】
矩阵的加法:行列数相等的各元素相加。
$\begin{bmatrix}{1}&{0}\\{2}&{5}\\{3}&{1}\end{bmatrix}+\begin{bmatrix}{4}&{0.5}\\{2}&{5}\\{0}&{1}\end{bmatrix}=\begin{bmatrix}{5}&{0.5}\\{4}&{10}\\{3}&{2}\end{bmatrix}$
矩阵的数乘:每个元素都要乘。
$3\times\begin{bmatrix}{1}&{0}\\{2}&{5}\\{3}&{1}\end{bmatrix}=\begin{bmatrix}{3}&{0}\\{6}&{15}\\{9}&{3}\end{bmatrix}=\begin{bmatrix}{1}&{0}\\{2}&{5}\\{3}&{1}\end{bmatrix}\times3$
Matrix Vector Multiplication【矩阵向量乘法】
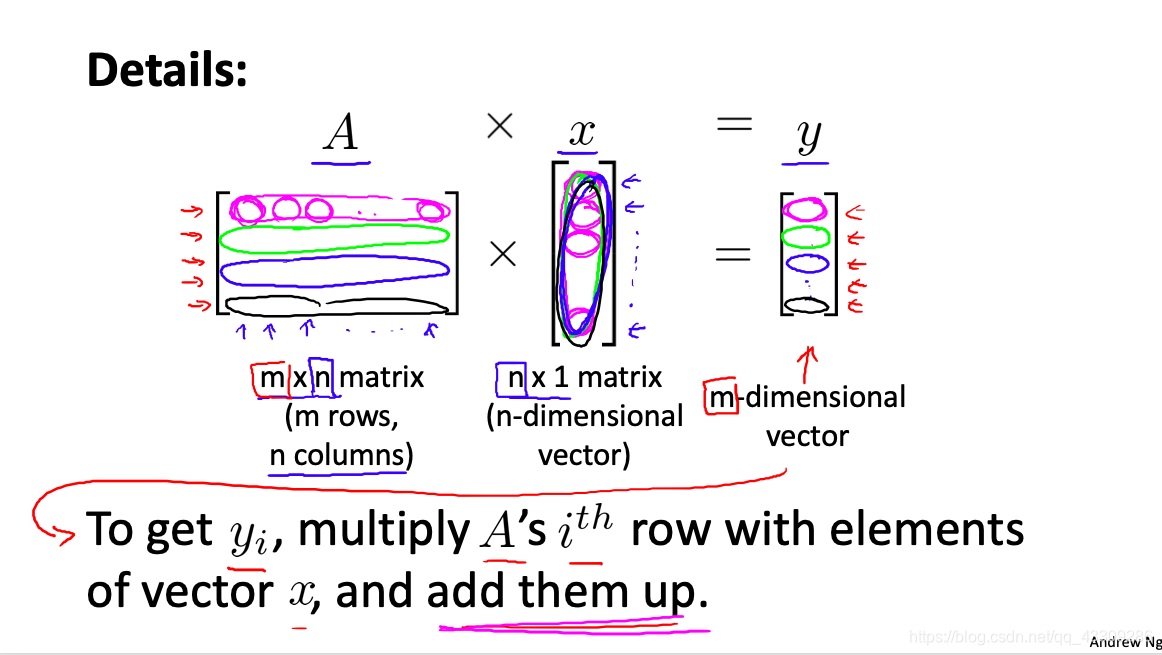
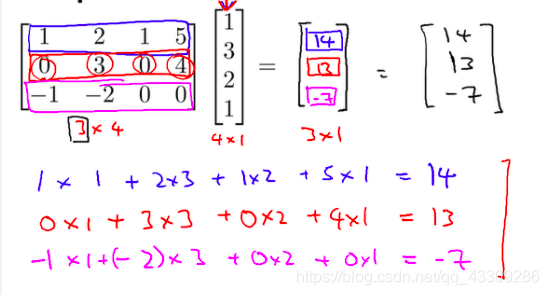
Matrix Matrix Multiplication【矩阵乘法】
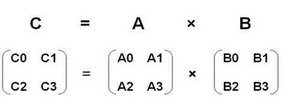
矩阵乘法:
$m×n$矩阵乘以$n×o$矩阵,变成$m×o$矩阵。


在单变量线性回归中的应用

Matrix Multiplication Properties【矩阵乘法的性质】
矩阵乘法的性质:
矩阵的乘法不满足交换律:$A×B≠B×A$
矩阵的乘法满足结合律。即:$A×(B×C)=(A×B)×C$
单位矩阵:在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,我们称这种矩阵为单位矩阵.它是个方阵,一般用 $I$ 或者 $E$ 表示,从左上角到右下角的对角线(称为主对角线)上的元素均为1以外全都为0
$A{{A}^{-1}}={{A}^{-1}}A=I$
对于单位矩阵,有$AI=IA=A$
Inverse and Transpose【逆、转置】
矩阵的逆:如矩阵$A$是一个$m×m$矩阵(方阵),如果有逆矩阵,则:$A{{A}^{-1}}={{A}^{-1}}A=I$
矩阵的转置:设$A$为$m×n$阶矩阵(即$m$行$n$列),第$i $行$j $列的元素是$a(i,j)$,即:$A=a(i,j)$
定义$A$的转置为这样一个$n×m$阶矩阵$B$,满足$B=a(j,i)$,即 $b (i,j)=a(j,i)$($B$的第$i$行第$j$列元素是$A$的第$j$行第$i$列元素),记${{A}^{T}}=B$。(有些书记为A’=B)
${{\begin{bmatrix} a& b \\ c& d \\ e& f \\\end{bmatrix} }^{T}}=\begin{bmatrix} a& c & e \ b& d & f \\\end{bmatrix}$
矩阵的转置基本性质:
$ {{\left( A\pm B \right)}^{T}}={{A}^{T}}\pm {{B}^{T}} $
${{\left( A\times B \right)}^{T}}={{B}^{T}}\times {{A}^{T}}$
${{\left( {{A}^{T}} \right)}^{T}}=A $
${{\left( KA \right)}^{T}}=K{{A}^{T}} $


